Электроника
Программный пакет для анализа информативности и интерпретации данных аэрозольных оптических измерений
Приведен пример анализа информативности данных поляризационного спектронефелометра. Проведена апробация полученных для интерпретации оптических измерений регрессионных соотношений на экспериментальном и расчетном материале AERONET.
Введение
Систематические измерения различных параметров аэрозолей как в натурных, так и в лабораторных условиях ведутся рядом научных коллективов уже около пятидесяти лет. Получено огромное количество экспериментального материала, выявлены многочисленные статистические зависимости между различными аэрозольными характеристиками. Однако получение надежных данных для требуемых практикой и научными задачами аэрозольных параметров в большинстве случаев продолжает оставаться проблематичным: аэрозоли чрезвычайно разнообразны и изменчивы по микроструктуре и физико-химическим свойствам, обработка результатов микрофизических измерений требует больших временных затрат, использования дорогостоящих приборов и систем. Косвенные методы определения микрофизических параметров аэрозоля (МФП) требуют измерения его оптических характеристик (ОХ), использования априорной информации при интерпретации результатов измерений и ее адекватности конкретной атмосферной ситуации, что далеко не всегда выполнимо.
Априорная информация может быть сформирована в виде общей микрофизической модели, содержащей основные сведения об исследуемых аэрозолях и позволяющей варьировать ее характеристики во всем диапазоне возможных изменений. При этом важнейшим является вопрос о возможности отражения этих изменений в измеряемых оптических характеристиках (ОХ), т.е. вопрос об информативности оптических измерений и о том, какие микрофизические параметры (МФП) аэрозоля могут быть в принципе получены с использованием существующих измерительных систем. Для планирования различных аэрозольных оптических измерений необходимо также решать задачу выбора набора измеряемых ОХ для определения конкретных МФП аэрозоля и оценки потенциальной точности определения последних.
Корреляционный подход к решению обратных задач
Решение задач оценок информативности исходных оптических измерений предлагается путем получения ансамбля реализаций оптических и микрофизических характеристик рассеивающей среды [1-3]. Данный ансамбль может быть получен при наличии достаточно большого объема экспериментальных данных по одновременным оптическим и микрофизическим измерениям. Однако комплекс оптических измерений всегда ограничен по спектральному диапазону, углам наблюдений и практически никогда не наблюдается полного соответствия оптических и микрофизических данных. Другой подход основывается на экспериментальных сведениях о возможных реальных вариациях микрофизических параметров частиц и последующем расчете необходимых оптических характеристик с "отсеиванием" тех реализаций, которые соответствуют не встречающимся в действительности значениям расчетных оптических и задаваемых микрофизических параметров среды [2]. Преимуществом такого подхода является возможность получения расчетных данных практически обо всех необходимых оптических параметрах аэрозоля в любом спектральном и угловом диапазонах. Далее рассчитываются ковариационные матрицы оптических и микрофизическиххарактеристик-D^HD соответственно, и кроссковариационная матрицы D между этими характеристиками. Используя данные матрицы, можно оценивать погрешности восстановления МФП с использованием метода линейных регрессий [4]:
x = i + D,v(D,:i+I52j'(y-y), (1)
где х - вектор искомых МФП, у - вектор измерений ОХ, I - единичная матрица, 8 - погрешность измерения ОХ. Влияние имеющейся априорной информации на точность интерпретации данных оптических измерений (сопутствующих микрофизических измерений) можно учитывать путем добавления в вектор у компонент, соответствующих измеряемым МФП.
Формула (1) используется в численных экспериментах по замкнутой схеме в целях восстановления МФП для множества реализаций параметров модели. Для каждой реализации по регрессионной формуле (1) для заданного набора измеряемых оптических характеристик Y с учетом добавления в их расчетные значения заданных погрешностей измерения рассчитываются значения МФП, которые сравниваются с их заданными значениями. После перебора всех реализаций вычисляются средние погрешности восстановления МФП. Исследование отношения средней погрешности определения конкретного МФП по измерению выбранных ОХ к его средней априорной вариации позволяет ранжировать измерения по информативности как относительно всего комплекса МФП, так и для каждого параметра индивидуально.
Данный подход позволяет решать задачи выбора конкретного набора измерений и оценки их требуемых точностей для определения конкретного МФП, а также оценивать потенциальную точность восстановления МФП с учетом особенностей реальной аппаратуры и имеющейся априорной информации.
На рис. 1 представлено главное меню программного пакета для анализа информативности оптических измерений, основанного на вышеизложенных принципах. Меню состоит из разделов ввода измеряемых ОХ, выбора типа аэрозоля (континентальный - фоновый и городской; морской; дымовой и пылевой), и подлежащих определению МФП и дополнительной априорной информации.
Универсальность программы обеспечивается возможностью рассмотрения любых комбинаций аэрозольных ОХ, реально осуществляемых на практике. В качестве указанных характеристик рассматривались объемные коэффициенты ослабления, обратного рассеяния, направленного рассеяния и степень линейной поляризации при рассеянии. Причем указанные характеристики могут измеряться в любой области спектрального диапазона от 0,3 до 15 мкм как на конкретных длинах волн, так и в заданных спектральных диапазонах. Для индикатрисы и степени поляризации могут быть выбраны любые углы или диапазоны углов. Задавая конкретные измерения, включая их точность, пользователь получает коэффициенты регрессионных соотношений между измеряемыми ОХ и определяемыми МФП аэрозоля и оценки потенциальной точности восстановления последних из оптических измерений, на основе которых можно делать выводы о требованиях к измерениям ОХ.
Для получения указанных регрессий используется база данных, включающая:
1)ансамбли МФП для основных типов (моделей) аэрозолей с использованием известных экспериментальных данных;
2)результаты расчетов ОХ и интегральных МФП для данных ансамблей. Континентальный и пылевой аэрозоли включают фракции, состоящие из несферических частиц, поэтому при расчете их ОХ используется модель хаотически ориентированных сфероидов, в которой в равной пропорции берутся сплющенные и вытянутые частицы с параметром формы, меняющемся в диапазоне от 1,2 до 2,2.
Поскольку при получении выборки микрофизических параметров путем их случайных вариаций могут получаться не встречающиеся в реальности расчетные значения как оптических, так и некоторых интегральных микрофизических характеристик, то чтобы "отфильтровать" выборку (т. е. исключить не встречающиеся в реальности значения отмеченных характеристик) накладывались ограничения на значения: коэффициента ослабления е (0,55), отношения коэффициентов обратного рассеяния Рл (0,55)^(1,02), параметра Ангстрема v, отношения объемных концентраций частиц грубодисперсной и тонкодисперсной фракций (для континентального аэрозоля), эффективного размера частиц аэрозоля и его фракций. Данные ограничения выбраны на основании анализа литературных данных, систематизированных в [5], и данных сети глобального мониторинга на основе сканирующих солнечных фотометров AERONET [6, 7].
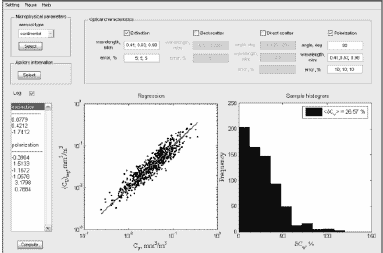
Рис. 1. Интерфейс программного пакета для анализа информативности аэрозольных оптических измерений
Пример анализа информативности оптических характеристик
В качестве примера использования разработанного программного пакета проведем анализ информативности данных поляризационного спектронефелометра, часто используемого в исследованиях аэрозолей, относительно МФП континентального аэрозоля [8, 9]. Будем считать, что проводятся измерения коэффициента направленного рассеяния под углом 45° на трех длинах волн полупроводниковых лазерных источников (0,41, 0,63 и 0,98 мкм) и его ортогональных поляризационных составляющих под углом 90° на двух длинах волн (0,41 и 0,63 мкм) с погрешностями -10 %.
Оптические измерения оказываются весьма информативными относительно восстановления параметров субмикронной фракции (с погрешностями примерно 24, 8 и 10 % соответственно для счетной N, объемной Сг концентраций и эффективного размера частиц rj). Это легко объяснимо физически, т.к. известен факт максимально сильного взаимодействия с излучением частиц в диапазоне размеров, близких к длине волны. Для мелко- и грубодисперсных фракций погрешности восстановления параметров N, Сул г составляют соответственно 560, 680, 15% и 44, 45,16%. Из приведенных оценок, следует, что погрешность восстановления полной счетной концентрации аэрозольных частиц практически соответствует ее априорному разбросу.
С высокой точностью восстанавливается вещественная часть комплексного показателя преломления (КПП) всех трех фракций аэрозоля (с погрешностями примерно 1,8% для мелко- и среднедисперсной фракций и 2,8 % для грубодисперсной). Мнимая же часть КПП восстанавливается хуже (погрешность порядка 50%), что объясняется существенно более слабой зависимостью от нее параметров аэрозольного рассеяния в видимом диапазоне спектра (ввиду малости мнимой части КПП основных аэрозольных веществ, за исключением сажи).
Для интерпретации данных рассматриваемых измерений получены регрессионные уравнения между измеряемыми ОХ и следующими МФП: действительная часть комплексных показателей преломления и эффективные размеры частиц трех аэрозольных фракций; счетная и объемная концентрации частиц средне- и грубодисперсной фракций. Данные уравнения были опробованы на массиве экспериментального и расчетного материала AERONET. Поскольку оптические характеристики, получаемые на станциях AERONET на основе измерений угловой зависимости яркости неба, являются интегральными по всему слою атмосферы, то имеет смысл проводить сравнение лишь для не зависящих от полной концентрации частиц аэрозоля параметров и работать с безразмерными комбинациями оптических характеристик (например, с отношениями спектральных значений коэффициентов рассеяния под углами 45° и 90° -Р45(0,41)/Р45(0,63); Р45(0,63)/Р45(0,98); Р90(0,41)/Р90(0,63)). Сравнение производилось по следующим микрофизическим параметрам: относительное содержание "мелких" частиц в объеме аэрозоля - VfIVt и эффективный размер частиц
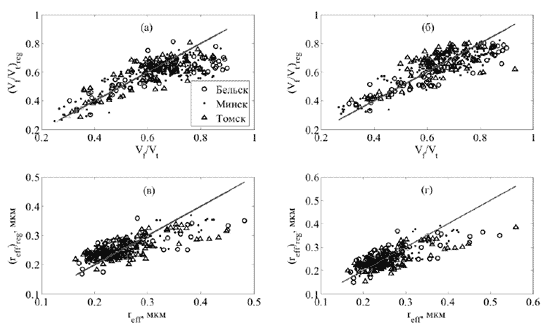
Рис.2 . Сопоставление результатов восстановления микрофизических параметров аэрозоля с использованием уравнений регрессий, полученных на основе статистической микрофизической модели (а, в) и рассматриваемого массива данных AERONET (б, г)
Регрессионные уравнения для этих параметров, полученные с использованием вышеописанного программного пакета, имеют вид:
На рис. 2а,в представлены результаты восстановления VIVt и reffc использованием уравнений (2) по оптическим характеристикам, полученным на станциях AERONET: г. Минск, Томск (городской аэрозоль) и г. Бельск (аэрозоль, ввиду малой антропогенной нагрузки региона близок по своим физико-химическим свойствам к фоновому). Для сравнения на рис. 2б,г показаны результаты восстановления данных параметров с использованием уравнений регрессий, полученных по исходному массиву данных AERONET.
Из рисунков видно хорошее соответствие результа-использовании уравнений (2) и 11,2, 10,5% при использовании уравнений, полученных по исходной выборке характеристик аэрозоля. Данные результаты подтверждают достоверность точностных оценок и уравнений регрессии, получаемых на основе численных расчетов.
Заключение
Таким образом, можно заключить, что разработанный программный пакет позволяет решать задачи интерпретации данных аэрозольных оптических измерений, оценивать потенциальную точность восстановления микрофизических параметров аэрозоля, ранжировать измерения по информативности и соответственно, оптимально планировать системы диагностики окружающей среды.
Литература:
1. Кугейко, М. М., Лысенко, С. А. Уравнения множественной регрессии для фракционных концентраций атмосферного аэрозоля и спектральных значений коэффициента ослабления // Журн. прикл. спектр. - 2006. - Т. 73. - №6. - С. 807.
2. Кугейко, М. М., Лысенко, С. А. Определение интегральных микрофизических параметров многокомпонентных аэрозолей по данным зондирования атмосферы локационными системами на основе Nd:YAG^a3epa // Оптика и спектроскопия. - 2009. - Т. 107. - №1. - С. 165-172.
3. Коршунов, В. А. О восстановлении интегральных параметров тропосферного аэрозоля по данным двух-волнового лидарного зондирования // Физика атмосф. и океана. - 2007. - Т. 43. - №5. - С. 671-687.
4. Колемаев, В. А., Калинина, В. Н. Теория вероятностей и математическая статистика. - М.: ИНФРА-М, 1997.-С. 302.
5. Кондратьев, К. Я., Ивлев, Л. С, Крапивин, В. Ф. Свойства, процессы образования и последствия воздействий атмосферного аэрозоля: от нано- до глобальных масштабов. - СПб: ВВМ. - 2007. - С. 807.
6. Cattrall, C., Reagan, J., Thome, K., Dubovic, O. Variability of aerosol spectral lidar and backscatter and extinction ratio of key aerosol types derived from selected Aerosol Robotic Network locations // J. Geophys. Res. -2005. - Vol. 110. - D10S11. - doi: 10.1029/2004JD005124.
7. http://aeronet.gsfc.nasa.gov.
8. Sviridenkov, M. A., Emilenko, A. S., Isakov, A. A., Kopeikin V.M. Comparison of Black Carbon Content, Aerosol Optical and Microphysical Characteristics in Moscow and the Moscow Region // Fifteenth ARM Science Team Meeting Proceedings, March 14-18, 2005 / Daytona Bech, Florida, 2005. - P. 140-147.
9. Панченко, М. В., Свириденков, М. А., Терпугова, С. А., Козлов, В. С. Активная спектронефелометрия в исследовании микрофизических характеристик субмикронного аэрозоля // Оптика атмосф. и океана. - 2004. - Т. 17. - №5-6. - С. 428-435.